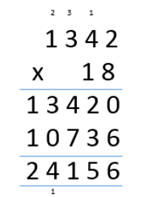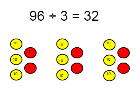Maths
Maths Curriculum Statement
What Maths looks like in Goodrich CE (VC) Primary School
Our aim is to equip all pupils with the skills and confidence to solve a range of problems through fluency with numbers and mathematical reasoning. Our ultimate aim is to ensure that children are given a visual/concrete representation of the maths being taught and set in a real-life context to make it meaningful to the children.
Throughout the school all classes are mixed age. We use a flexible mastery approach which is taught with the lesson objective chosen from each year group which closely match and are a continuation of each other being developed throughout the lesson or series of lessons. Where lesson objectives for differing year groups cannot be closely match, objectives are taught to the whole class ensuring that support and/or depth of learning opportunities are provided. When necessary and appropriate, children are taught in smaller groups for precision teaching.
|
CURRICULUM INTENT |
Curriculum Intent What Maths looks like in our school. ❖ A curriculum which caters for the needs of all individuals ❖ A flexible approach is adopted to the grouping of children based on their needs relating to the particular objective(s) being taught. Where appropriate children are given the opportunity to choose the level of their challenge based on their need and thus providing opportunities for them to develop as independent learners. ❖ Daily basic skills practise (Mastering number/Minute Maths/ 9 Quick Questions / Times Tables) to ensure fluency and develop long term recall ❖ We use a concrete, pictorial, abstract approach (see Calculation Policy) ❖ Regular Reasoning & Problem-solving opportunities are provided ❖ Questioning is a key part of the maths lesson – letting the children demonstrate what they know and challenging them every step ❖ Pupils are required to explore maths in depth, using mathematical vocabulary to reason and explain their workings ❖ A well planned lessons using ready-to-progress criterion for each year group which links to pupils’ prior knowledge and future applications. ❖ Structured interventions to help close the gaps for targeted children.
This is our philosophy: ❖ To become fluent in the fundamentals of mathematics so that children develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately. ❖ To be able to solve problems by applying their mathematics to a variety of problems with increasing sophistication, including in unfamiliar contexts and to model real-life scenarios ❖ To reason mathematically by following a line of enquiry and develop and present a justification, argument or proof using mathematical language. ❖ To have an appreciation of number and number operations, which enables mental calculations and written procedures to be performed efficiently, fluently and accurately to be successful in mathematics.
This is the knowledge and understanding gained at each stage: By the end of EYFS pupils will: ❖ Have a deep understanding of number to 10, including the composition of each number ❖ Subitise (recognise quantities without counting) up to 5 ❖ Automatically recall (without reference to rhymes, counting or other aids) number bonds up to 5 (including subtraction facts) and some number bonds to 10, including double facts ❖ Verbally count beyond 20, recognising the pattern of the counting system ❖ Compare quantities up to 10 in different contexts, recognising when one quantity is greater than, less than or the same as the other quantity ❖ Explore and represent patterns within numbers up to 10, including evens and odds, double facts ❖ Develop their spatial reasoning skills across all areas of mathematics including shape, space and measures ❖ Have an ability to look for patterns and relationships, spot connections, ‘have a go’, talk to adults and peers about what they notice and not be afraid to make mistakes.
By the end of Key Stage 1 pupils will: ❖ Develop confidence and mental fluency with whole numbers, counting and place value. ❖ Use numerals, words and the four operations, including with practical resources. ❖ Recognise, describe, draw, compare and sort different shapes and use the related vocabulary. ❖ a range of measures to describe and compare different quantities such as length, mass, capacity/volume, time and money. ❖ know the number bonds to 20 and be precise in using and understanding place value. An emphasis on practice at this early stage will aid fluency. ❖ Read and spell mathematical vocabulary, at a level consistent with their increasing word reading and spelling knowledge at key stage 1
By the end of Lower Key Stage 2 pupils will: ❖ Be increasingly fluent with whole numbers and the four operations, including number facts and the concept of place value. ❖ Develop efficient written and mental methods and perform calculations accurately with increasingly large whole numbers. ❖ Develop their ability to solve a range of problems, including with simple fractions and decimal place value. ❖ Draw with increasing accuracy and develop mathematical reasoning so they can analyse shapes and their properties and confidently describe the relationships between them. ❖ Use measuring instruments with accuracy and make connections between measure and number. ❖ By the end of year 4, memorised their multiplication tables up to and including the 12 multiplication table. ❖ Read and spell mathematical vocabulary correctly and confidently, using their growing word reading knowledge and their knowledge of spelling.
By the end of Key Stage 2 pupils will: ❖ Understand the number system and place value to include larger integers. ❖ Make connections between multiplication and division with fractions, decimals, percentages and ratio. ❖ Develop their ability to solve a wider range of problems, including increasingly complex properties of numbers and arithmetic, and problems demanding efficient written and mental methods of calculation. ❖ Use the language of algebra as a means for solving a variety of problems. ❖ Classify shapes with increasingly complex geometric properties and use the vocabulary they need to describe them. ❖ Be fluent in written methods for all four operations, including long multiplication and division, and in working with fractions, decimals and percentages. ❖ Read, spell and pronounce mathematical vocabulary correctly
|
|
CURRICULUM IMPLEMENTATION |
Curriculum Implementation
Please refer to:
This is how it works:
This is what the adults do:
This how we support:
This is how we support staff:
This how we challenge:
This how we ensure all children can access the curriculum:
Cultural Capital/Enrichment
The mathematics curriculum allows our pupils to develop lifelong skills that are essential for succeeding in all aspects of school life and beyond. Cultural Capital is the essential knowledge that children need to prepare them for their future success – in the world of work, in relationships forged throughout life and as a valued contributor to society. Therefore, our aim is to give children the knowledge and skills to prepare them for what comes next in their lives. This includes the relevant vocabulary needed throughout their education and the opportunity to link maths to real-world problem solving.
Cultural Capital is the accumulation of knowledge, behaviours, and skills that a child gains over time through different experiences and opportunities. They draw upon these to demonstrate their cultural awareness, knowledge and competence. It is one of the key ingredients a child will draw upon to be successful in society, their career and the world of work. Cultural Capital gives a child power. It helps them achieve goals, become successful, and rise up the social ladder without necessarily having wealth or financial capital.
We recognise that for a child to aspire and be successful academically and in the wider areas of their lives, they need to be given rich and sustained opportunities to develop. Within Maths, we engage in; Careers Information, Growth mindset, Resilience development strategies and Pupil Voice to empower pupils. |
|
CURRICULUM IMPACT |
Curriculum Impact
This is what you might typically see:
This is how we know how well our children are doing:
We have identified substantive and disciplinary knowledge which is fundamental to the children’s development and understanding as mathematicians. They accumulate this as they move through our school which then gives them a firm foundation to build on when they move on to KS3 and beyond.
This is the impact of the teaching:
|
Maths Progression Document
Overview Goldcrests
|
MATHS |
Wk 1 |
Wk 2 |
Wk 3 |
Wk 4 |
Wk 5 |
Wk 6 |
Wk 7 |
Wk 8 |
Wk 9 |
Wk 10 |
Wk 11 |
Wk 12 |
|||
|
Autumn |
Spatial Awareness Number songs/rhymes/stories |
||||||||||||||
|
Pattern (Families) |
Number and Measure (Covered through the themes of Senses Healthy Eating and Harvest) |
Number, Measure and Pattern (Harvest) |
Shape (Diwali) |
Number and Shape (Bonfire Night) |
Number (Hibernation and Christmas) |
||||||||||
|
Spring |
Spatial Awareness Number songs/rhymes/stories |
||||||||||||||
|
Pattern
(Winter) |
Number and Measure (Seasons, Rhyme and Story Telling) |
Shape and Pattern (Chinese New Year) |
Number (Friends and Pets) |
Number and Measure (Mother’s Day) |
Pattern and Shape (Volcanoes) |
Number, Measure and Pattern (Easter) |
Spatial Awareness Number songs/rhymes/stories |
||||||||
|
Summer |
Spatial Awareness Number songs/rhymes/stories |
||||||||||||||
|
Pattern (Frogs) |
Number, Shape and Measure (Size) |
Number (Life Cycles, Insects and Wild animals) |
Number and Measure (Pets and Growing) |
Shape (Other Cultures) |
Pattern (Transition) |
Number and Measure (Three Billy Goats Gruff) |
Number (Emotions) |
||||||||
Overview Wrens– Reception
|
MATHS |
Wk 1 |
Wk 2 |
Wk 3 |
Wk 4 |
Wk 5 |
Wk 6 |
Wk 7 |
Wk 8 |
Wk 9 |
Wk 10 |
Wk 11 |
Wk 12 |
|
Autumn |
Number: song/rhymes Spatial Awareness Baseline assessments |
Number: Weeks 1 – 6 mastering Number (4 days per week) Spatial awareness, Pattern, Shape and Measure: on going through continuous provision and focused teaching one day per week. |
Consolidation |
|||||||||
|
Spring |
Number: Weeks 7 – 16 mastering Number (4 days per week) Spatial awareness, Pattern, Shape and Measure: on going through continuous provision and focused teaching one day per week.
|
Consolidation |
||||||||||
|
Summer |
Number: Weeks 17 – 25 mastering Number (4 days per week) Spatial awareness, Pattern, Shape and Measure: on going through continuous provision and focused teaching one day per week. |
Consolidation |
||||||||||
|
MATHS |
Wk 1 |
Wk 2 |
Wk 3 |
Wk 4 |
Wk 5 |
Wk 6 |
Wk 7 |
Wk 8 |
Wk 9 |
Wk 10 |
Wk 11 |
Wk 12 |
|
Autumn |
Number: Place value Y1 – Numbers to 20 Y2 – Numbers to 100 |
Number: Addition and Subtraction Y1 – Numbers within 20 (including recognising money) Y2 – Numbers within 100 (including money) |
Number: Y1 – Place value to 50 and Multiplication Y2 - Multiplication |
|||||||||
|
Spring |
Number: Y1 Division and consolidation Y2 Division |
Number: Y1 – place value to 100 Statistics Y2 - Statistics |
Measurement: Length and Height |
Geometry: Y1 – Shape and consolidation Y2 – Properties of Shape |
Number: Y1 - Fraction and consolidation Y2 - Fraction |
Consolidation |
||||||
|
Statistics Y2 - Statistics |
||||||||||||
|
Summer |
Geometry: Position and Direction |
Measurement: Time |
Number: Y1 – Place Value recap |
Number: Y1 – Four operations consolidation |
Measurement: Y1 - Weight and Volume Y2 - Mass, Capacity and Temperature
|
Geometry: Y1 – Properties of Shape (Y2 objectives) Y2 – Properties of Shape (Y3 objectives) |
||||||
|
Number: Y2 – problem Solving |
Number: Y2 – Four operations problems solving and investigations |
|||||||||||
Overview Woodpeckers – Year 3 and 4
|
MATHS |
Wk 1 |
Wk 2 |
Wk 3 |
Wk 4 |
Wk 5 |
Wk 6 |
Wk 7 |
Wk 8 |
Wk 9 |
Wk 10 |
Wk 11 |
Wk 12 |
|
|
Aut |
Number: Place value |
Number: Addition and Subtraction |
Number: Multiplication and Division |
||||||||||
|
Spring |
Number: Multiplication and Division
|
Measurement: Length, Perimeter and Area (+ Fractions recap) |
Number: Fractions |
Number: Decimals (including money) |
Consolidation |
||||||||
|
Summer |
Measurement: Time, Mass and Capacity
|
Statistics |
Assessments and consolidation |
Geometry: Properties of Shape including Position and Direction (current year groups objectives plus following year’s objectives) |
Consolidation of any objectives from the year/ moving onto following year’s objectives |
||||||||
Overview Owls - Year 4 and 5
|
MATHS |
Wk 1 |
Wk 2 |
Wk 3 |
|
Wk 4 |
Wk 5 |
Wk 6 |
Wk 7 |
Wk 8 |
Wk 9 |
Wk 10 |
Wk 11 |
Wk 12 |
|
|
Autumn |
|
Number: Place value |
Number: Addition and Subtraction |
Number: Multiplication and Division |
Measurement: Length, Perimeter and Area (+ Fractions recap) |
|||||||||
|
Spr |
Number: Multiplication and Division |
|
Number: Fractions and Decimals |
|||||||||||
|
Summer |
Statistics
|
|
Number: Fractions, Decimals and Percentages |
Assessments and consolidation |
Geometry: Properties of Shape (current year groups objectives plus following year’s objectives)
|
Consolidation of any objectives from the year/ moving onto following year’s objectives |
||||||||
Overview Peregrines – Year 5 and 6
|
MATHS |
Wk 1 |
Wk 2 |
Wk 3 |
Wk 4 |
Wk 5 |
Wk 6 |
Wk 7 |
Wk 8 |
Wk 9 |
Wk 10 |
Wk 11 |
Wk 12 |
|
Autumn |
Number: Place value
|
Number: All Four Operations |
Number: Fractions, Decimals and Percentages |
Measurement: Area, Perimeter and Volume |
||||||||
|
Spring |
Number: Multiplication and Division |
Number: Algebra |
Geometry: Properties of Shape |
Statistics |
Measurement: Time and Money |
Ratio and Proportion |
||||||
|
Summer |
Consolidation |
Y5 Properties of shape |
Y5 consolidate All four operations |
Y5 Measurement - Angles |
Consolidation of any objectives from the year/ moving onto following year’s objectives |
|||||||
|
Y6: SATS |
Y6 Cross Curricular topic work |
|||||||||||
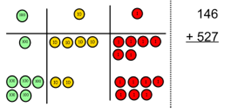
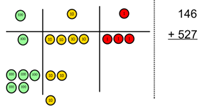
Addition
|
Objective and Strategies |
Concrete |
Pictorial |
Abstract |
|||
|
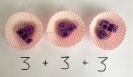
Combining two parts to make a whole: part- whole model |
|
Use pictures to add two numbers together as a group or in a bar.
|
4 + 3 = 7 10= 6 + 4
Use the part-part whole diagram as shown above to move into the abstract. |
|||
|
Starting at the bigger number and counting on |
Start with the larger number on the bead string and then count on to the smaller number 1 by 1 to find the answer. |
12 + 5 = 17
Start at the larger number on the number line and count on in ones or in one jump to find the answer. |
5 + 12 = 17 Place the larger number in your head and count on the smaller number to find your answer.
|
|||
|
Regrouping to make 10.
|
6 + 5 = 11
Start with the bigger number and use the smaller number to make 10. |
Use pictures or a number line. Regroup or partition the smaller number to make 10.
|
7 + 4= 11
If I am at seven, how many more do I need to make 10. How many more do I add on now? |
|||
|
Adding three single digits |
4 + 7 + 6= 17 Put 4 and 6 together to make 10. Add on 7.
Following on from making 10, make 10 with 2 of the digits (if possible) then add on the third digit. |
Add together three groups of objects. Draw a picture to recombine the groups to make 10. |
Combine the two numbers that make 10 and then add on the remainder. |
|||
|
Column method- no regrouping
|
24 + 15= Add together the ones first then add the tens. Use the Base 10 blocks first before moving onto place value counters.
|
After practically using the base 10 blocks and place value counters, children can draw the counters to help them to solve additions.
|
|
|||
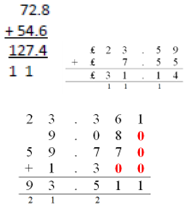
|
Column method- regrouping
|
Make both numbers on a place value grid.
Add up the units and exchange 10 ones for one 10.
Add up the rest of the columns, exchanging the 10 counters from one column for the next place value column until every column has been added. This can also be done with Base 10 to help children clearly see that 10 ones equal 1 ten and 10 tens equal 100. As children move on to decimals, money and decimal place value counters can be used to support learning.
|
Children can draw a pictoral representation of the columns and place value counters to further support their learning and understanding.
|
Start by partitioning the numbers before moving on to clearly show the exchange below the addition.
As the children move on, introduce decimals with the same number of decimal places and different. Money can be used here.
|
Subtraction
|
Objective and Strategies |
Concrete |
Pictorial |
Abstract |
|
Taking away ones |
Use physical objects, counters, cubes etc to show how objects can be taken away.
|
Cross out drawn objects to show what has been taken away.
|
18 -3= 15 8 – 2 = 6 |
|
Counting back |
Make the larger number in your subtraction. Move the beads along your bead string as you count backwards in ones.
13 – 4 Use counters and move them away from the group as you take them away counting backwards as you go.
|
Count back on a number line or number track
Start at the bigger number and count back the smaller number showing the jumps on the number line.
This can progress all the way to counting back using two 2 digit numbers. |
Put 13 in your head, count back 4. What number are you at? Use your fingers to help. |
|
Find the difference |
Compare amounts and objects to find the difference.
Use cubes to build towers or make bars to find the difference Use basic bar models with items to find the difference. |
Count on to find the difference.
Draw bars to find the difference between 2 numbers. |
Hannah has 23 sandwiches, Helen has 15 sandwiches. Find the difference between the number of sandwiches. |
|
Part Part Whole Model
|
Link to addition- use the part whole model to help explain the inverse between addition and subtraction. If 10 is the whole and 6 is one of the parts. What is the other part? 10 - 6 = |
Use a pictorial representation of objects to show the part part whole model.
|
Move to using numbers within the part whole model. |
|
Make 10
|
14 – 9 =
Make 14 on the ten frame. Take away the four first to make 10 and then takeaway one more so you have taken away 5. You are left with the answer of 9. |
Start at 13. Take away 3 to reach 10. Then take away the remaining 4 so you have taken away 7 altogether. You have reached your answer. |
16 – 8= How many do we take off to reach the next 10? How many do we have left to take off? |
|
Column method without regrouping |
Use Base 10 to make the bigger number then take the smaller number away.
Show how you partition numbers to subtract. Again make the larger number first. |
Draw the Base 10 or place value counters alongside the written calculation to help to show working.
|
|
|
Column method with regrouping |
Use Base 10 to start with before moving on to place value counters. Start with one exchange before moving onto subtractions with 2 exchanges.
Make the larger number with the place value counters
Start with the ones, can I take away 8 from 4 easily? I need to exchange one of my tens for ten ones.
Now I can subtract my ones.
Now look at the tens, can I take away 8 tens easily? I need to exchange one hundred for ten tens.
Now I can take away eight tens and complete my subtraction
Show children how the concrete method links to the written method alongside your working. Cross out the numbers when exchanging and show where we write our new amount.
|
Draw the counters onto a place value grid and show what you have taken away by crossing the counters out as well as clearly showing the exchanges you make.
When confident, children can find their own way to record the exchange/regrouping. Just writing the numbers as shown here shows that the child understands the method and knows when to exchange/regroup. |
Moving forward the children use a more compact method.
This will lead to an understanding of subtracting any number including decimals.
|
Multiplication
|
Objective and Strategies |
Concrete |
Pictorial |
Abstract |
|
Doubling |
Use practical activities to show how to double a number. |
Draw pictures to show how to double a number. |
Partition a number and then double each part before recombining it back together. |
|
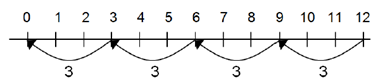
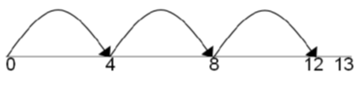
Counting in multiples |
Count in multiples supported by concrete objects in equal groups. |
Use a number line or pictures to continue support in counting in multiples.
|
Count in multiples of a number aloud. Write sequences with multiples of numbers. 2, 4, 6, 8, 10 5, 10, 15, 20, 25 , 30
|
|
Repeated addition |
Use different objects to add equal groups. |
|
Write addition sentences to describe objects and pictures. |
|
Arrays- showing commutative multiplication |
Create arrays using counters/ cubes to show multiplication sentences.
|
Draw arrays in different rotations to find commutative multiplication sentences.
Link arrays to area of rectangles.
|
Use an array to write multiplication sentences and reinforce repeated addition.
|
|
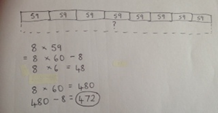
Grid Method |
Show the link with arrays to first introduce the grid method.
4 rows of 10 4 rows of 3 Move on to using Base 10 to move towards a more compact method.
4 rows of 13
Move on to place value counters to show how we are finding groups of a number.We are multiplying by 4 so we need 4 rows.
Fill each row with 126.
Add up each column, starting with the ones making any exchanges needed.
Then you have your answer. |
Children can represent the work they have done with place value counters in a way that they understand.
They can draw the counters, using colours to show different amounts or just use circles in the different columns to show their thinking as shown below. |
Start with multiplying by one digit numbers and showing the clear addition alongside the grid.
Moving forward, multiply by a 2 digit number showing the different rows within the grid method.
|
|
Column multiplication |
Children can continue to be supported by place value counters at the stage of multiplication.
It is important at this stage that they always multiply the ones first and note down their answer followed by the tens which they note below. |
Bar modelling and number lines can support learners when solving problems with multiplication alongside the formal written methods.
|
Start with long multiplication, reminding the children about lining up their numbers clearly in columns. If it helps, children can write out what they are solving next to their answer.
This moves to the more compact method.
|
Division
|
Objective and Strategies |
Concrete |
Pictorial |
Abstract |
||||||||||||
|
Sharing objects into groups |
I have 10 cubes, can you share them equally in 2 groups? |
Children use pictures or shapes to share quantities.
8 ÷ 2 = 4 |
Share 9 buns between three people.
9 ÷ 3 = 3 |
||||||||||||
|
Division as grouping |
Divide quantities into equal groups. Use cubes, counters, objects or place value counters to aid understanding.
|
Use a number line to show jumps in groups. The number of jumps equals the number of groups.
Think of the bar as a whole. Split it into the number of groups you are dividing by and work out how many would be within each group. |
28 ÷ 7 = 4
Divide 28 into 7 groups. How many are in each group?
|
||||||||||||
|
Division within arrays |
Link division to multiplication by creating an array and thinking about the number sentences that can be created.
Eg 15 ÷ 3 = 5 5 x 3 = 15 15 ÷ 5 = 3 3 x 5 = 15 |
Draw an array and use lines to split the array into groups to make multiplication and division sentences. |
Find the inverse of multiplication and division sentences by creating four linking number sentences.
7 x 4 = 28 4 x 7 = 28 28 ÷ 7 = 4 28 ÷ 4 = 7 |
||||||||||||
|
Division with a remainder |
14 ÷ 3 = Divide objects between groups and see how much is left over
|
Jump forward in equal jumps on a number line then see how many more you need to jump to find a remainder.
Draw dots and group them to divide an amount and clearly show a remainder.
|
Complete written divisions and show the remainder using r.
|
||||||||||||
|
Short division |
Use place value counters to divide using the bus stop method alongside
42 ÷ 3= Start with the biggest place value, we are sharing 40 into three groups. We can put 1 ten in each group and we have 1 ten left over.
We exchange this ten for ten ones and then share the ones equally among the groups.
We look how much in 1 group so the answer is 14. |
Students can continue to use drawn diagrams with dots or circles to help them divide numbers into equal groups.
Encourage them to move towards counting in multiples to divide more efficiently. |
Begin with divisions that divide equally with no remainder.
Move onto divisions with a remainder.
Finally move into decimal places to divide the total accurately.
|
Maths Assessment
Children are assessed within lessons on a daily basis. Frequent opportunities are built into lessons to assess children’s retention of previous objectives taught to ensure that the objectives are securely achieved (the daily number skills sessions are ideal opportunities for this assessment.)
Progress through objectives are recorded on data sheets termly. Analysis of this data is completed shortly after each data point and used to inform teaching and learning.
Evidence for assessment could also include:
- Children’s work
- Marking codes and annotations
- Teacher/TA observation notes
- Photographs with annotations
- Audio recordings
- End of unit tasks
Essential Building Blocks
Knowledge of number facts and a fluency in using them is a vital part of Maths for each year group. Rapid recall of number facts can provide the basic knowledge required for most aspects of primary mathematics, including mental and written calculations, fractions, decimals and percentages and problem solving. Number facts learned in Maths can also be transferred to many other subjects across the curriculum and in ‘real life’ situations.
|
Year |
Essential Building Blocks |
|
EYFS |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
Maths Vocabulary
Core Maths Vocabulary: All Classrooms to have these where relevant to learning.
Digit, integer, number, answer, solution, solve, work out, systematic, group, share, sort, diagram, represent, pattern, relationship, rule, sequence, explain, correct, incorrect, true, false, agree, disagree, same, different, bar model, part- whole model, formal method, equal to, more, less, greater than, fewer, less than, largest, greatest, least, most, estimate, approximately.
|
|
Number- Place Value |
Number- Addition and Subtraction |
Number- Multiplication and Division |
Number- Fractions |
Measurement |
Geometry- Shape |
Geometry-Position and direction |
Statistics |
|
EYFS
|
Number; zero; numbers to 20; count, forwards, backwards; how many, more, fewer, equal, group; order, largest, smallest, less; even, odd |
One more, one less, altogether, how many are left? Same, different, number bond, part-whole, add, take-away |
Double, half, halve, halving, pairs, twice as many, share, equal, unequal, group, left over |
Half, halve, halving |
Now, before, soon, later, after, next, fastest; time, yesterday, today, tomorrow, day, week, weekend, month, year; Days of the week: Monday, Tuesday, etc. Seasons: spring, summer, autumn, winter; birthday, holiday; Morning, afternoon, evening, night, midnight bedtime, dinner/lunch time, playtime; length, height, breadth, tall, short, long, tallest, shortest, longest, longer/shorter, taller/shorter, wider/narrower, weigh, weight, heavy, heavier, heaviest, light, lighter, lightest, balance |
Shape, circle, triangle, rectangle, square, side, straight, curved, cylinder, cube, cuboid, cone, sphere, pyramid, face, same, different, pattern. |
On, next to, over, under, around, through. |
|
|
Year 1 |
Numbers to 100; place value; digit, integer; symbol; compare; equal to, more, less, greater than, fewer, less than, greatest, smallest; first, second, third…last; ones, tens, partition, exchange; order, largest, smallest, biggest, least, most.
|
Number bonds, part, whole; plus; fact family, addition sentence, number sentence; how many more; number line; commutative; addition, more, make, sum, total, add together, altogether; calculation; Inverse equals, is the same as (including equals sign); subtract, , subtraction, take away, minus; difference between, what is the difference? how many more?, how many less? how much more is? |
How many altogether? How may are there?; groups, groups of, equal groups, unequal groups; row, column, array; number sentence; double, doubles; equal groups of 2, equal groups of 5, equal groups of 10; share, sharing, equally, odd, even, |
Whole, parts, equal parts, the same; split; groups; share; equally; quarter; four equal parts One half, two halves A quarter, two quarters |
Length, measure, measuring; ruler, cm; mass; balance, scale; volume, full, half full, quarter full, empty; capacity; holds, Container; money; value; coin; note; amount; 1p, 2p, 5p, 10p, 20p, 50p, £1, £2, £5, £10; hour, o'clock, half past, clock, watch, hands; hour, minute, second; before, after next, last now, soon, early, late quick, quicker, quickest, quickly, fast, faster, fastest, slow, slower, slowest, slowly old, older, oldest, new, newer, newest
|
Polygon, 2D, 3D, group, sort, corner (point, pointed) Face, side, edge Make, build, draw. |
Turn, full, half, quarter, three quarter; direction; movement, move; position; left, right, up, down; top, bottom, middle, above, below, between; in front, behind.
|
|
|
Year 2 |
2-digit; base 10; pattern; sequence; Numbers to one hundred Hundreds Partition, recombine Hundred more/less |
Bar model; operation, inverse operation; column; exchange; bridge; method; |
Times-table; facts; multiples; repeated addition; lots of; of; multiply; multiplied by; times; commutative; twos, fives, tens, threes; array; go into; divide, divide between, division, dividing; grouping, sharing; |
Two quarters, three quarters, one third, two thirds; unit fraction, numerator, denominator, vinculum; equivalence, equivalent. |
Change, total; distance; metres; g/kg; ml/l; temperature, thermometer, degrees Celsius, increase, decrease, warmer, colder; quarter past/to, 5 past, 10 past, twenty to etc, start, duration, end, interval, how long…? When did it start /end /finish…?, seconds; |
Pentagon, hexagon, octagon, quadrilateral; prism; vertices, vertex; rotate; Symmetry, symmetrical, line of symmetry; horizontal, vertical; Fold; pattern, repeating pattern. |
Direction, forwards, backwards; right angle; rotation, Clockwise, anticlockwise. |
Count, tally, tally chart, table; data, represent, sort; pictogram, symbol; block diagram, axis; label, title, scale; most popular, most common, least popular, least common; Venn diagram, Carrol diagram. |
|
Year 3 |
Numbers to one thousand; 3-digit; thousand; ascending, descending;
|
Column, column addition and subtraction; regroup; efficient; estimate.
|
Fours, eights; remainder; divisor, dividend, quotient.
|
Non-unit fraction; tenths, two tenths, three tenths etc; two thirds; fifth, sixth, ninth; decimal, decimal point; |
mm; perimeter; leap year; minutes past/to; a.m., p.m.; analogue, digital; twelve-hour /twenty-four- hour clock; Roman numerals I to XIII. |
Parallel, perpendicular; surface; acute angle, obtuse angle. |
North, South, East, West; angle, point, acute, obtuse; ninety degrees Orientation (same orientation, different orientation) |
Chart, bar chart; frequency table, Carroll diagram,
Diagram |
|
Year 4 |
Numbers to ten thousand; Roman numerals to one hundred; round, nearest; approximately; negative, minus, count through zero; tenths, hundredths, 0.25, 0.5, 0.75. |
Formal method. |
Sixes, sevens, nines; produce, poduct; commutativity; factor, factor pair; formal method; |
Proper fraction, improper fraction, mixed number; hundredths;
|
Km; rectilinear; area, square centimetres; warmest, coldest. |
Isosceles, scalene, equilateral; rhombus, parallelogram, trapezium; regular polygon; mirror line, reflect. |
Coordinates, translation, first quadrant, x-axis, y-axis.
|
Continuous data, discrete data; line graph, x axis, y-axis.
|
|
Year 5 |
Numbers to a million; Roman numerals to one thousand; powers of 10.
|
Place holder. |
Common factor, prime number, composite number, prime factor, square number, cubed number; round up/down.
|
Common denominator; thousandth; simplify, simplified; convert; per cent, percentage, per hundred; |
Imperial units, metric units, inches, lbs, pints; timetable; compound shape; volume, capacity, cm cubed/cubic cm. |
Degrees, protractor, reflex angle; irregular polygon, dimensions; net. |
Reflection, reflect. |
|
|
Year 6 |
Numbers to ten million.
Algebra: Function, input, output; algebra, algebraic, rule; expression; substitute; formula, formulae; equation; value, possible values.. |
|
Order of operations, BIDMAS; common multiple, lowest common multiple. |
Cancel, highest common factor, common numerator.
Ratio, proportion; for every ?_there are_, :(to); enlargement, scale factor. |
Tonnes, ounces, stone, miles. |
Vertically opposite (angles), internal angles; circumference, radius, diameter, centre. |
Four quadrants. |
Mean, pie chart. |
Maths Recommended Reads/ Websites/ Apps
Early Years and Key Stage 1 Maths
A selection of great counting books and maths stories covering cardinal and ordinal numbers and place value.
|
The Great Pet Sale by Mick Inkpen
|
One to Ten and Back Again by Nick Sharratt
|
The Shopping Basket by John Burningham
|
The Doorbell Rang by Pat Hutchins
|
|
Ten Black Dots by Donald Crews
|
I Spy Numbers By Jean Marzollo
|
Mouse Count by Ellen Stoll Walsh
|
The Hueys in None the Number by Oliver Jeffers
|
Recommended reads for Key Stage 2 Maths
These books are a great way to introduce a range of mathematical concepts like pie charts, probability, ratio and simplifying fractions in a way which engages the children in a story.
|
A Remainder of One by Elinor Pinczes
|
Fractions in Disguise by Edward Einhom
|
Spaghetti and Meatballs for All by Marilyn Burns
|
A Very Improbable Story by Edward Einhom
|
|
Sir Cumference and the Off the Charts Dessert by Cindy Neuschwander
|
Sir Cumference and the Dragon of Pi by Cindy Neuschwander
|
The Cavern of Clues by David Glover
|
Recommended Websites - Click the images to visit!
|
Maths Playground |
Multiplication Grand Prix |
Times Tables |
|
Times Tables Rockstars |
Topmarks – Hit the button |
Topmarks – Maths |
|
ICT games |
Maths Frame |
Primary Homework Help |
|
BBC Bitesize KS1 |
BBC Bitesize KS2 |
|
Recommended Apps |
||
|
|
|
|
|
White Rose 1 minute app |
White Rose 1 minute app wall chart (to print) |
|